Definitions
this document is under construction
By definition a sudoku puzzle of size 9x9 has
Rows, columns and blocks are referred to as regions and each region contains 9 cells
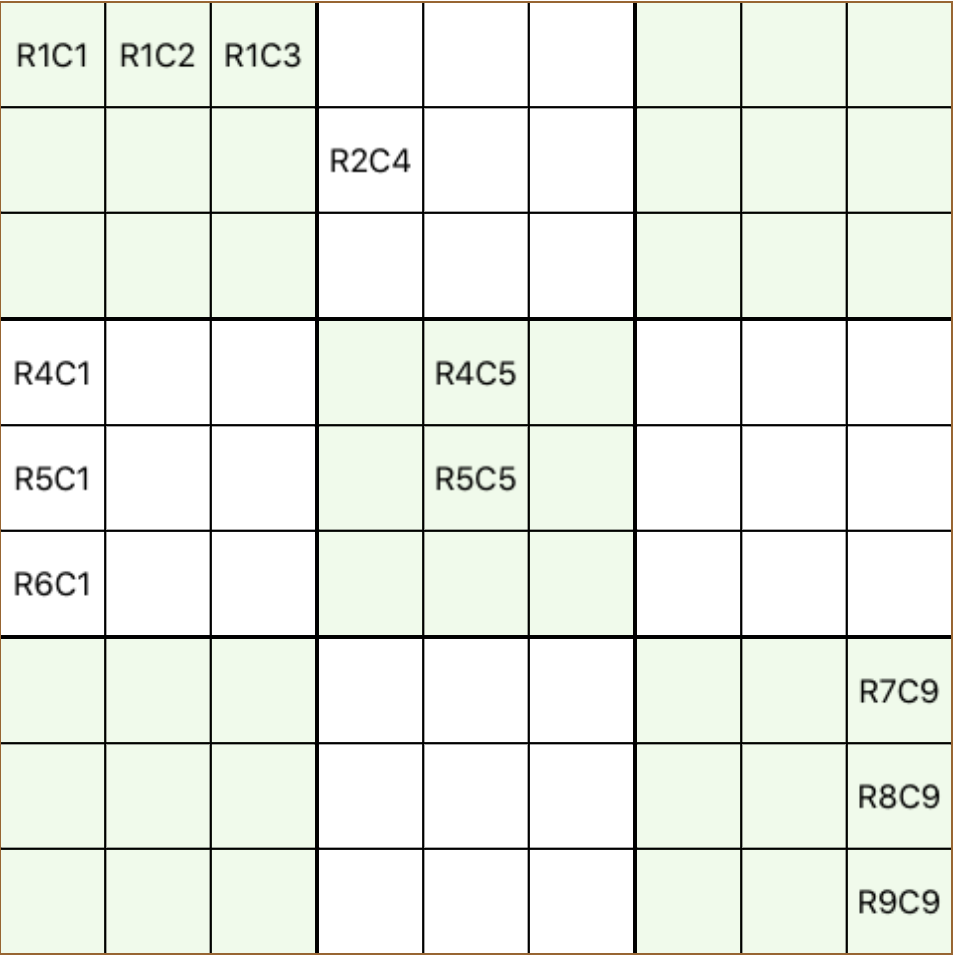
Cells are identified by their row and column as the examples shown in the following grid
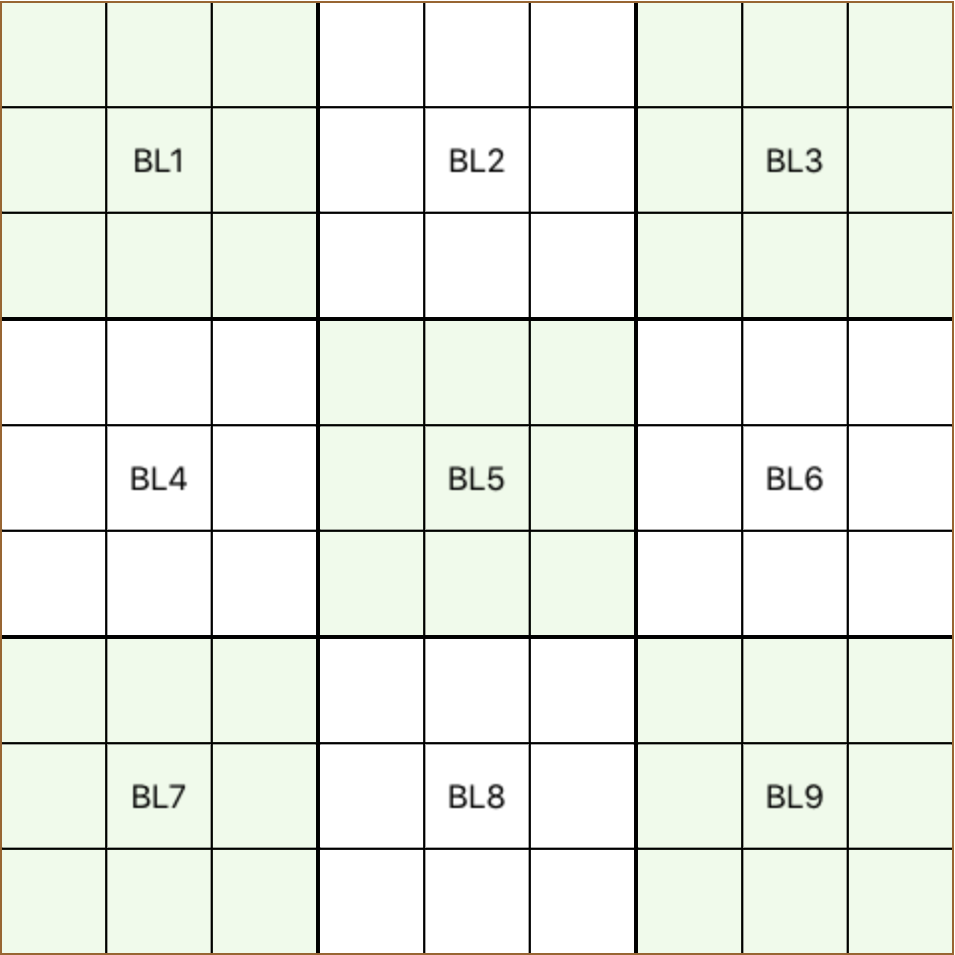
the 9 blocks
each row has 1 and only common cell with each column and each column has 1 and only common cell with each row also each row and column has 3 common cells with each of 3 particular blocks in a solved puzzle, the 9 cells of each region must contain a number from 1 to 9 this means that a number appears only once in a row, once in a column and only once in a block, but each appearance in a row counts for one appearance in one column and at the same time counts for an appearance in a block, the column with which a referenced row shares a common cell and the block in which the common cell lives, so ultimately there are only 9 appearances of each number in the whole grid and this provides:
The Basic Rule
each cell in a region (row, column or block) must contain a different number
A cell without a number we say it is empty,
Empty cells have a set of candidate numbers to be inserted,
this set of candidates, is assumed from the numbers already inserted in the other cells of the regions in which the empty cell is contained
A cell with only one candidate number is implied, which is, it is clear that a particular number is correct for this cell and the candidate is referred to as a
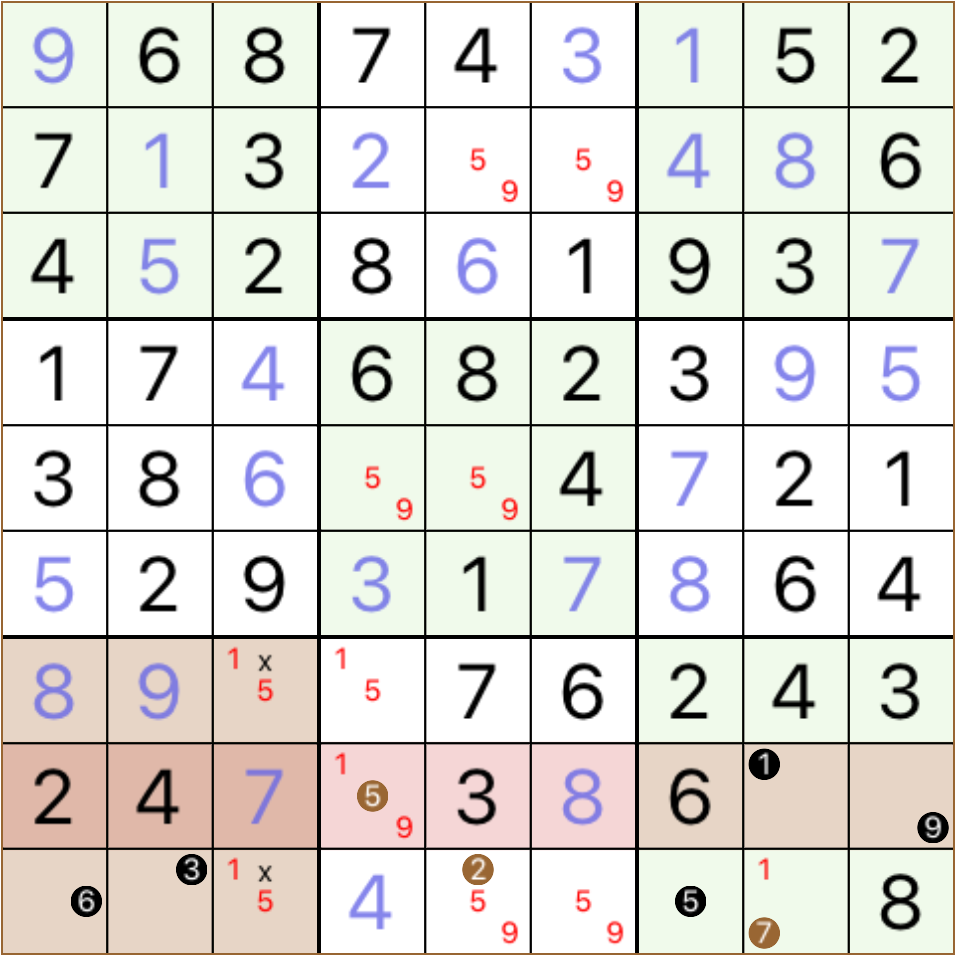
in a region, when there is only one cell containing a particular candidate, then this cell must have this number as its solution in this case we also say that this cell is implied, and this candidate is referred to as a Hidden Single for that region the above grid shows R8 (row 8) having a candidate for 5 only in R8C4, so although there are other candidates, 1 and 9, for R8C4 the correct solution is only number 5 please notice the naked singles of 6 for R9C1, 3 for R9C2, 1 for R8C8, 9 for R8C9 and 5 for R9C7 and the hidden singles of 5 in R8C4 for R8, 2 in R9C5 for R9, C5 and BL8 and 7 in R9C8 for R9, C8 and BL9 ..
one more definition that has to take place, as it is referenced quite often in this tutorial, is the notion of block-row and block-column structures as mentioned, each row and column crosses 3 blocks each, having 3 common cells with each one these 3 blocks define a block-row, when is covering 3 rows, and a block-column when they cover 3 columns in the following grig block-row 1 and block-column 2 are shaded

Logic
facing a sudoku puzzle, questions about cells and regions, numbers and candidates arise. pointing to a particular cell, a first question may be:
what is the correct solution for this cell ?
in order to imply the solution for a selected cell, we can presuppose that all candidates are possible then investigating the three regions in which the cell belongs, the row, the column and the block, which altogether we may call the cell's 'neighbourhood', we may find some numbers already in the cells of the neighbourhood, which we may call 'neighbours' each of the found numbers can be excluded from the possible candidates of our selected cell finally, if there is only one candidate left not being excluded from our investigation, then this implies that this candidate is the correct solution for our cell and this is the case that we have a Naked Single look at this example, R2C7 has only one candidate and this is number 1
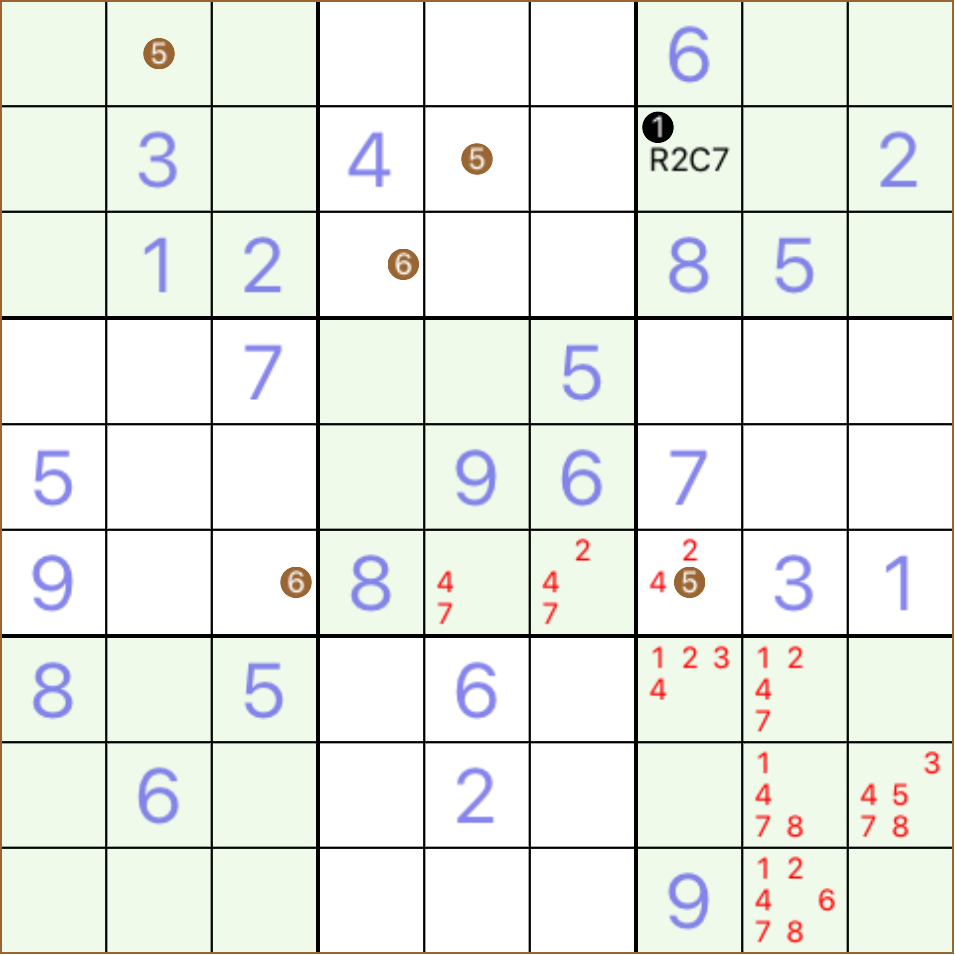
so number 1 is a naked single for R2C7, whilst numbers 2, 3 and 4 exist in the same row, number 5 exist in the same block and numbers 6, 7, 8 and 9 exist in the same column the following grid shows three more naked singles 1, 3 and 9 in cells R3C8, R4C9 and R5C7 respectively
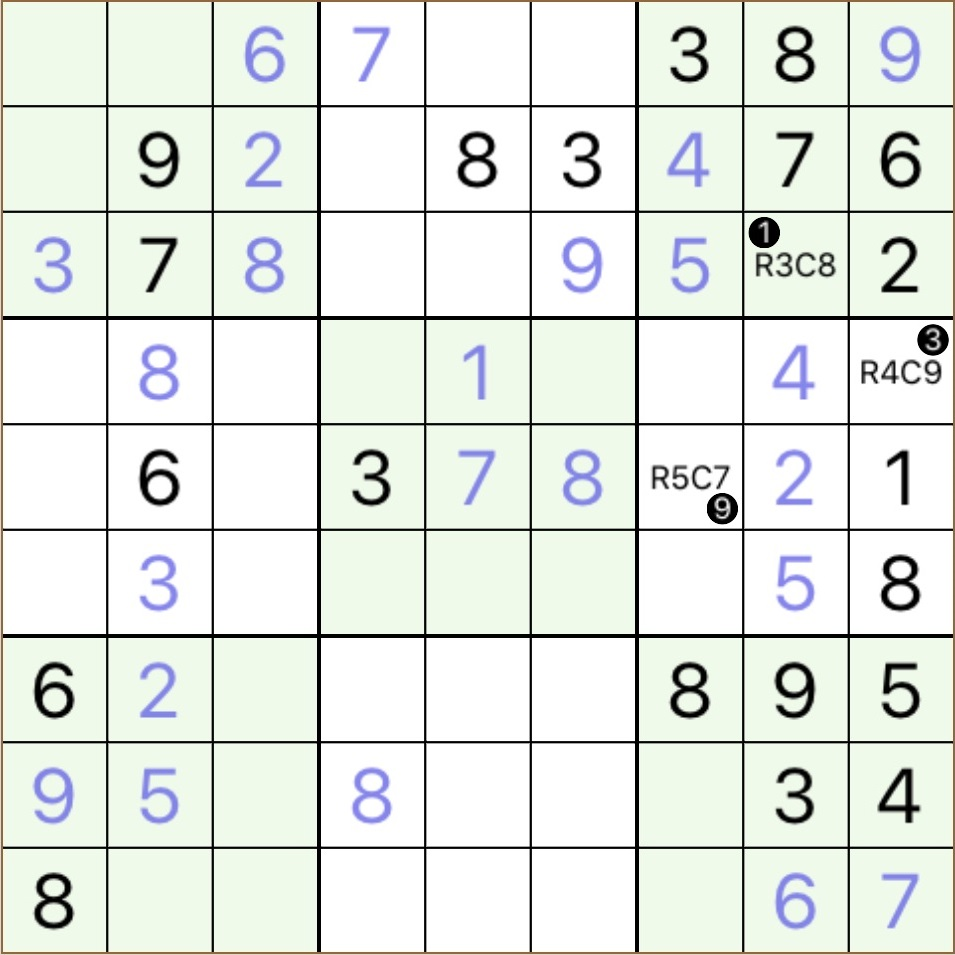
thus, in order to find a naked single, we focus on a cell presupposing all candidates possible, then investigating it's neighbours, we start excluding candidates until there is only one left although determining if a cell has a naked single or not, is logically easy, you need to search each cell one by one, and after each move again from the beginning, in order to solve all cells by excluding the presupposed candidates, stepping on the existing numbers of the same neighbourhood but that's all we can do answering the preceding question of 'what is the correct solution for this cell ?' focusing on a particular region, an other question may arise: where hides a particular number in this region ? and although it seems more complicated by the previous, answering requires fewer investigations look at this grid again
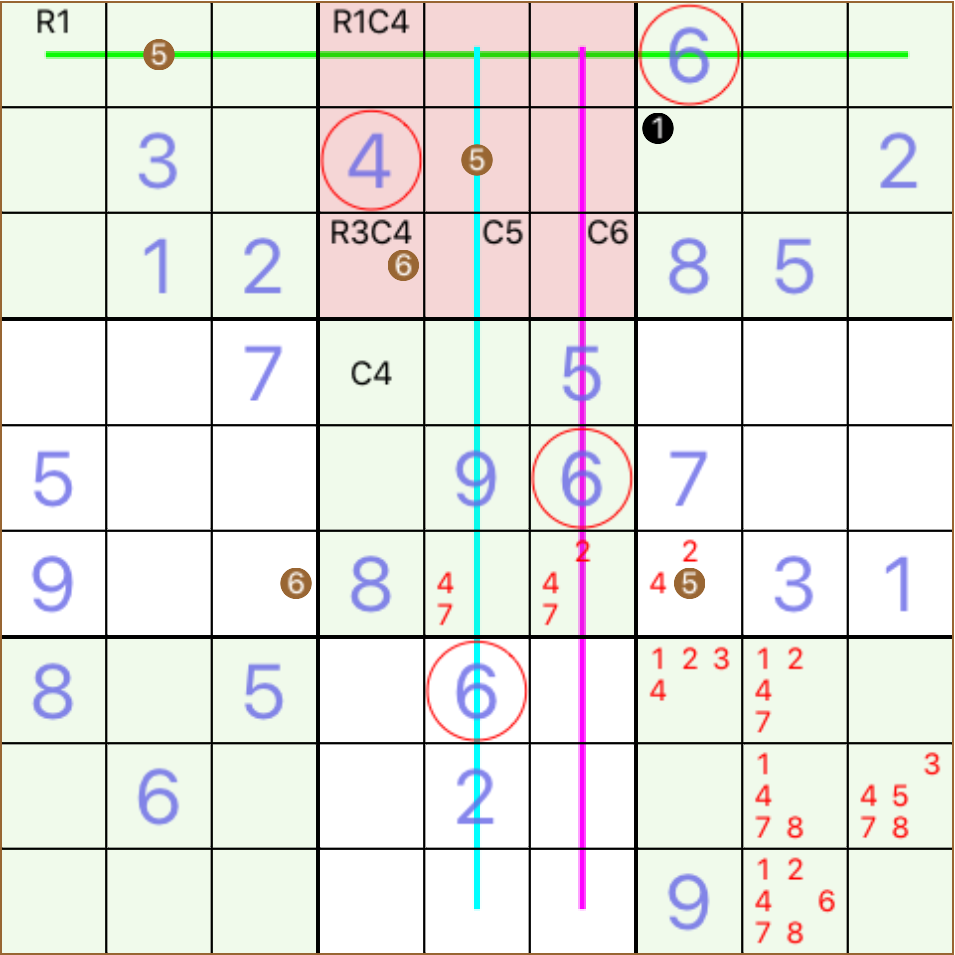
there are two 6s in block-column 2
one is in BL5 and C6 (magenta)
and the second in BL8 and C5 (cyan)
these two facts imply that BL2 (the shaded block) can contain candidates for a 6 only in column 4
but there is one more 6 in R1C7
this implies that R1C4 can not be 6 and whilst R2C4 is occupied by a 4, the only cell in BL2 that can contain a 6 is the cell R3C4
so, the answer for the question 'where 6 is hidden in BL2 ?' is 'in R3C4'
and this exposes the case of a 'Hidden Single'
some more examples
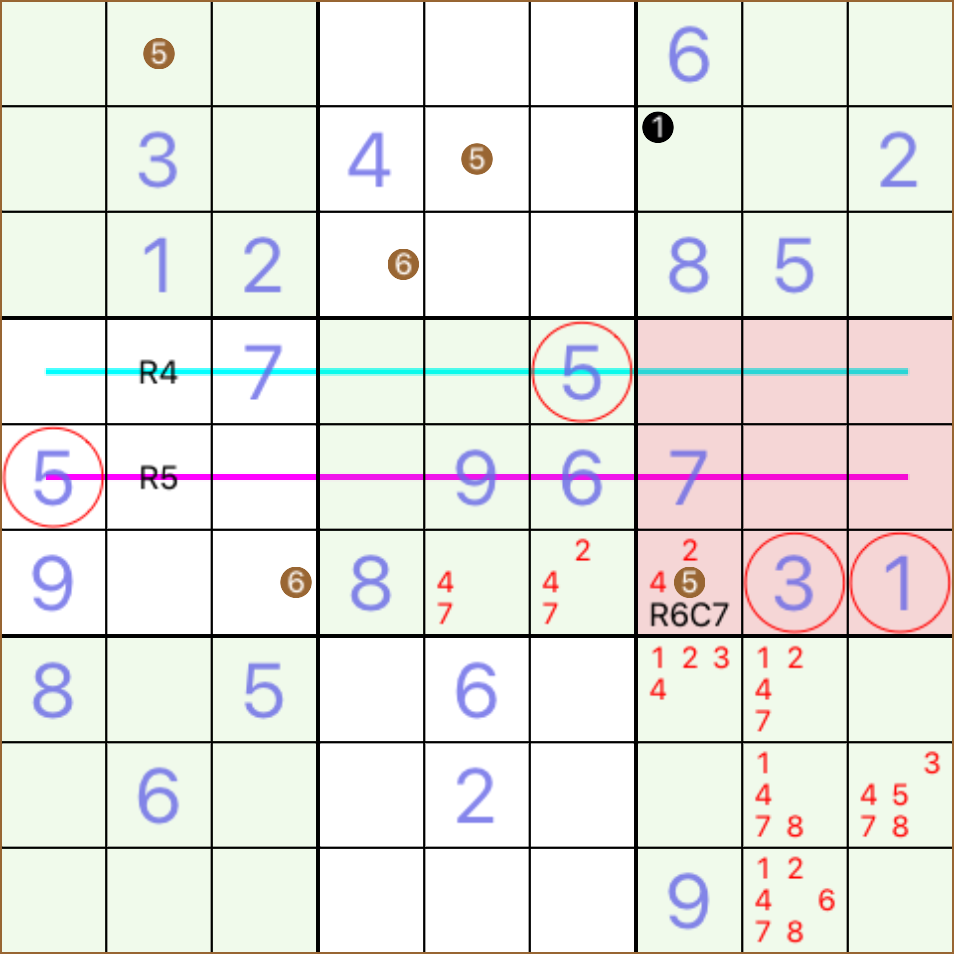
these two 5s in rows R4 and R5 prohibit including 5 in the candidates for cells in their neighbourhoods which include some cells in BL6 BL6 is left with only one cell that can take a 5, the cell R6C7, whilst R6C8 and R6C9 are occupied by 3 and 1 so the 5 for BL6 hides in that cell and this is an other case of a hidden single one more
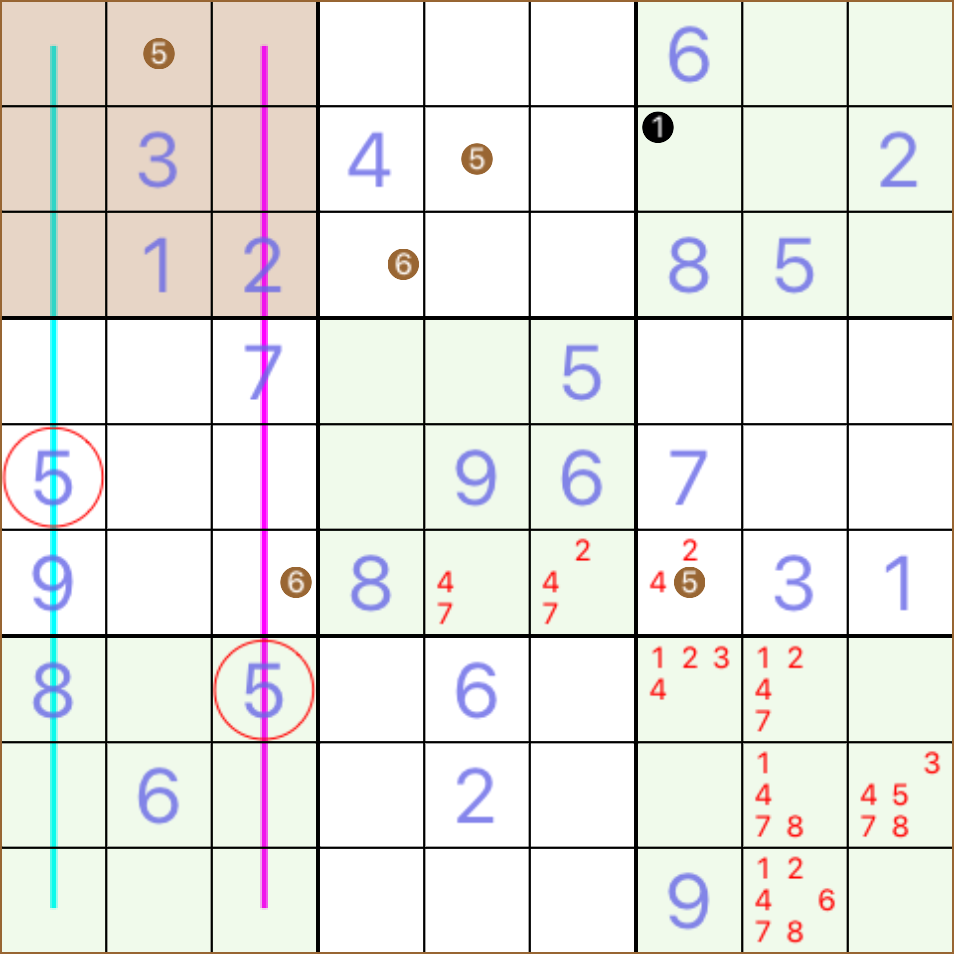
5 can only be in R1C2 for BL1 and for C2 hidden in a row
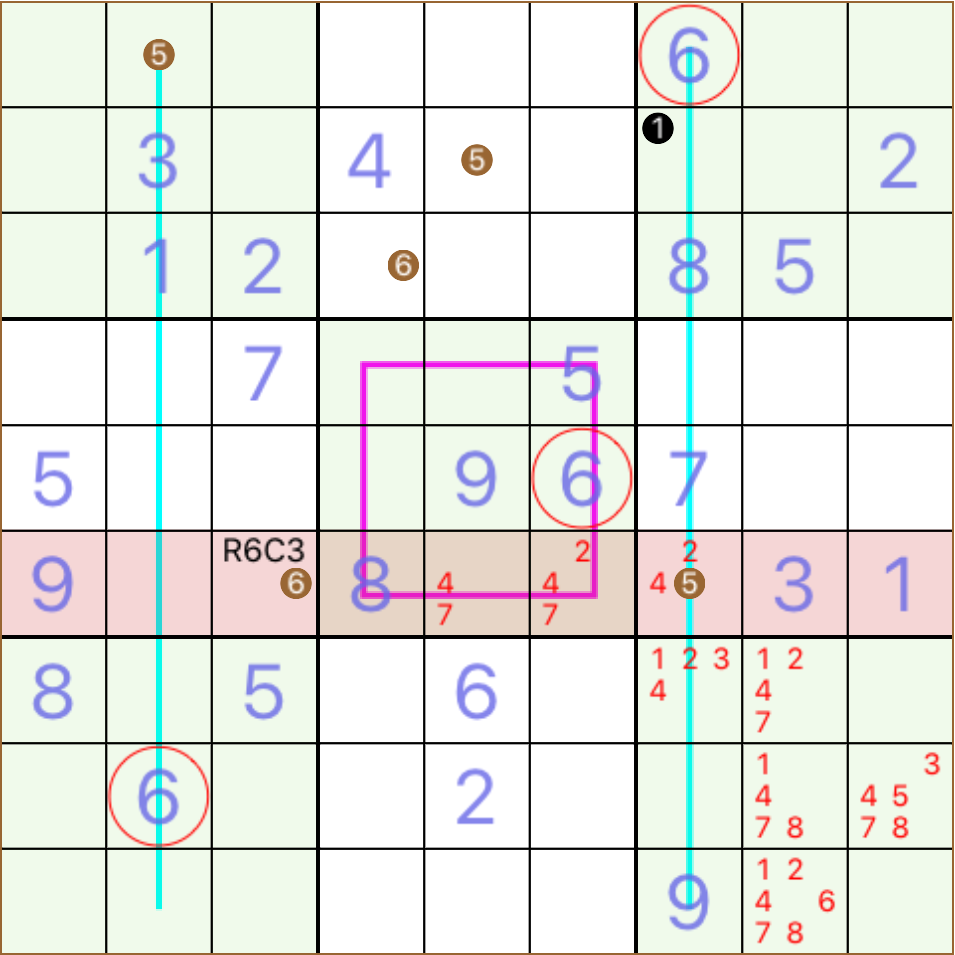
look at the shaded R6, all empty cells of this row, except R6C3, have a neighbour containing 6, this is why none of them have a candidate for 6 R6C3 contains the hidden single of R6 for number 6 hidden in a column
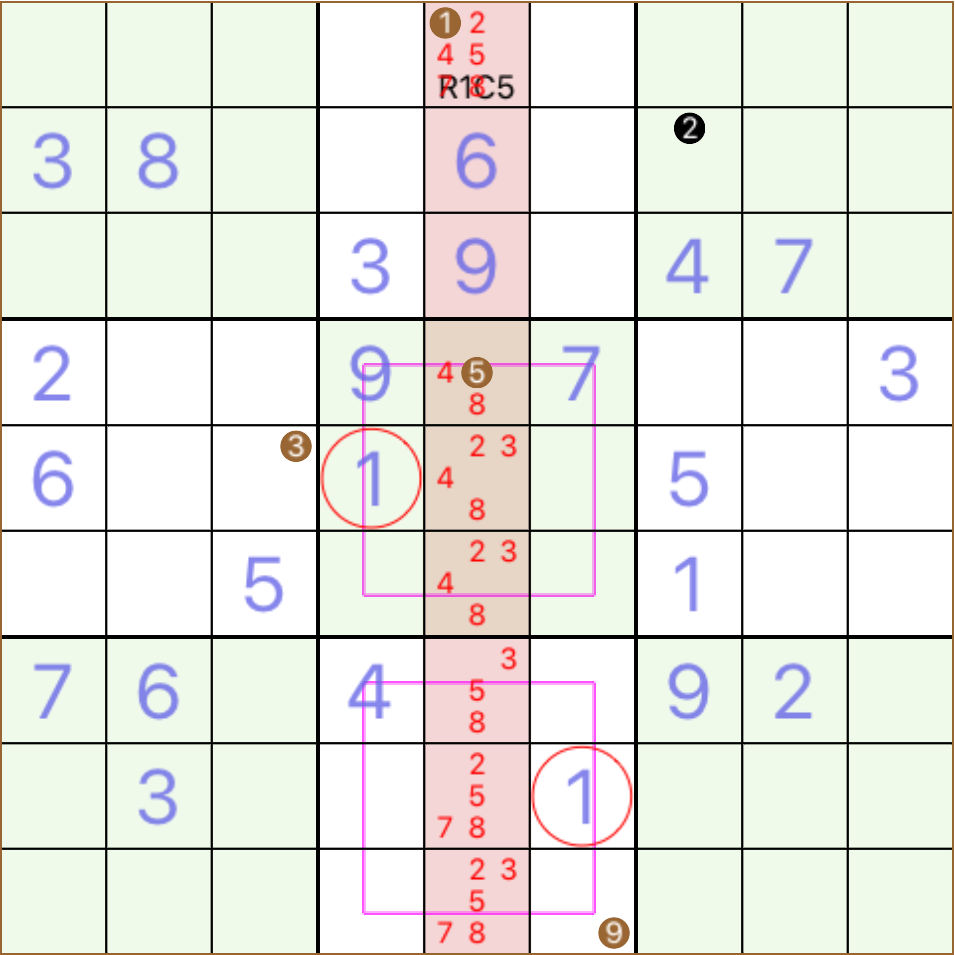
look at the shaded C5, all empty cells of this column, except R1C5, have a neighbour containing 1, this is why none of them have a candidate for 1 R1C5 contains the hidden single of C5 for number 1 the same puzzle forwarded
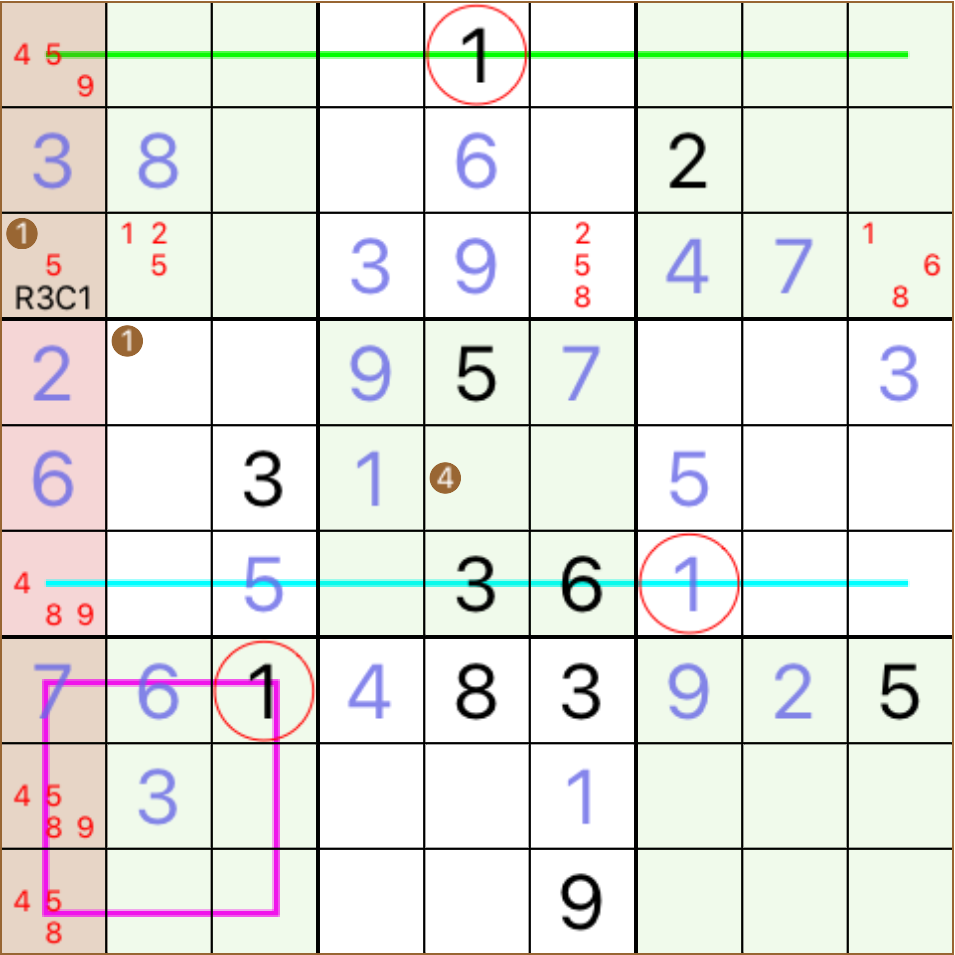
look at the shaded C1, all empty cells of this column, except R3C1, have a neighbour containing 1, this is why none of them have a candidate for 1 R3C1 contains the hidden single of C5 for number 1 forming a method indeed, scanning regions to reveal hidden singles seems much easier than counting candidate one by one, in order to find naked singles what we have done so far, is to look for a number in cells of the grid, that appears more often than others and then pay attention to the neighbourhood of each cell in order to exclude candidates of this number from all neighbours the cases examined in previous examples seem quite different in the sense that one is targeting a row in order to reveal a hidden single, others are targeting a column or a block also, we used a variant number of already given or solved cells in order to imply the solution for an other cell these facts do not help us to form a method that reveals hidden singles, but they rather provide a number of cases requiring a similar approach * one case popular in the easy puzzles, is when there are two appearances of a number in the same structure of block-row
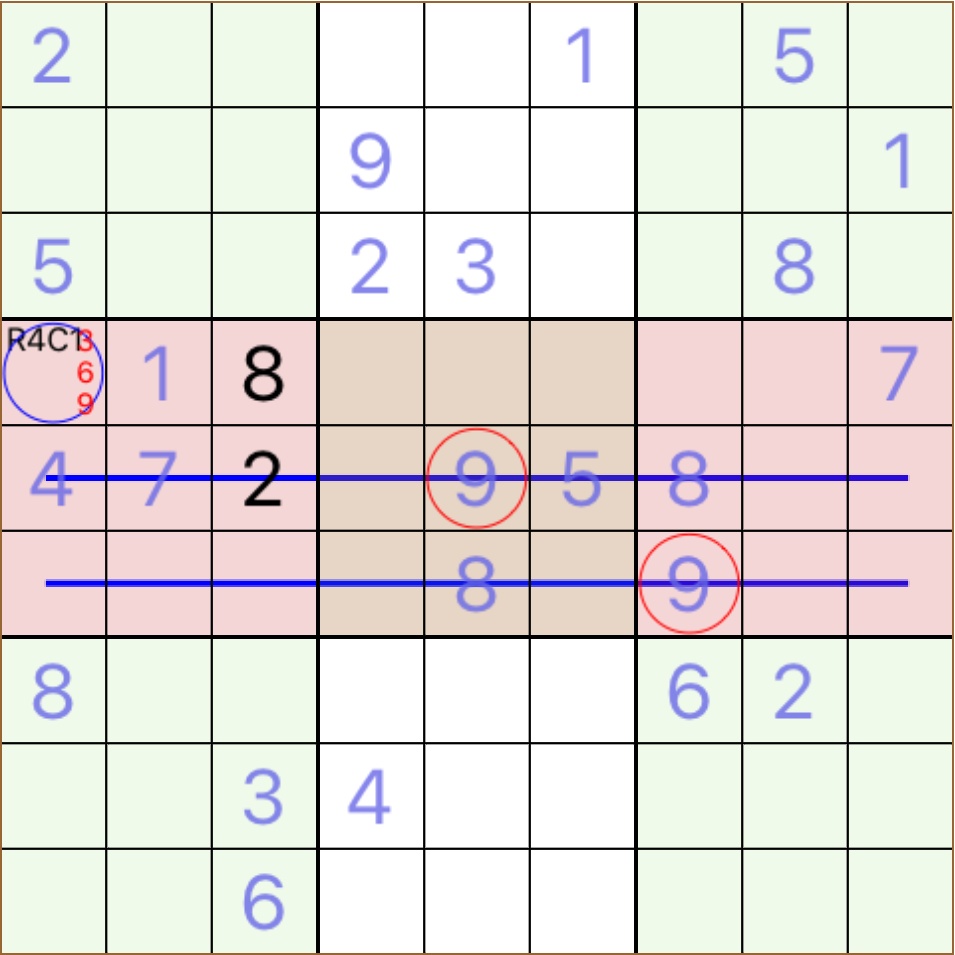
R4C1 must take 9 or block-column
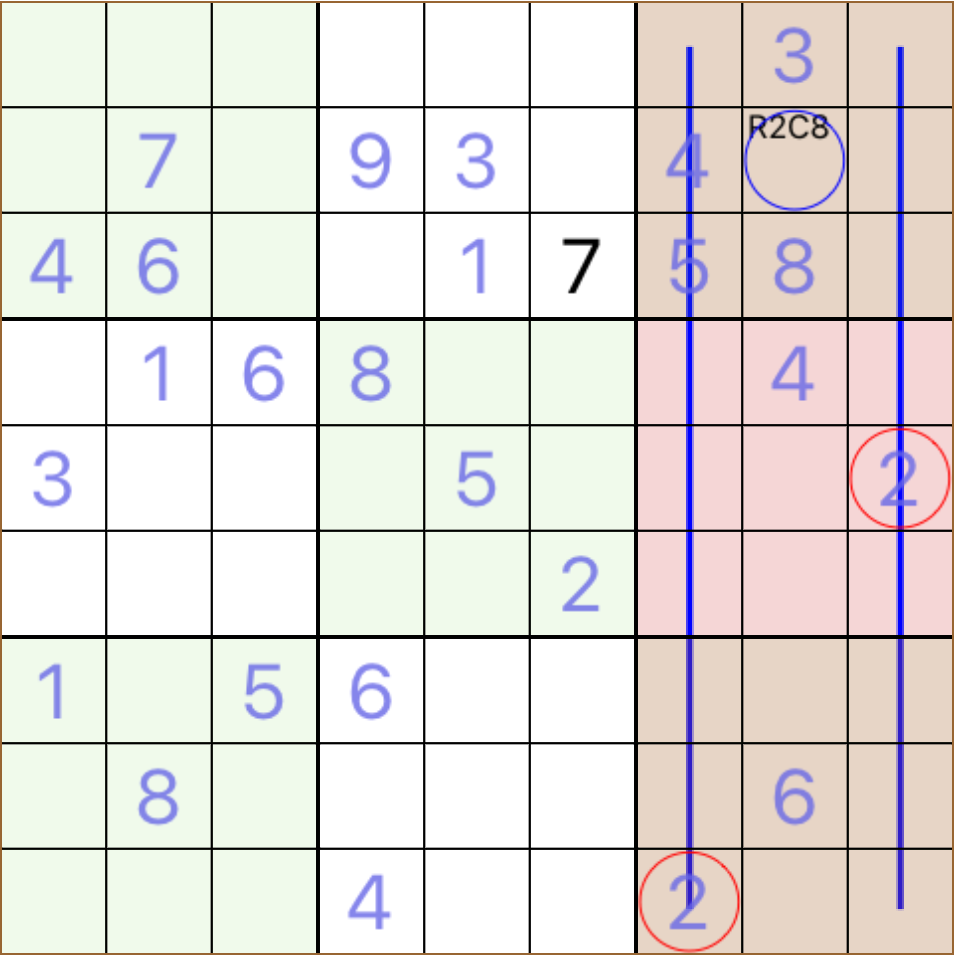
R2C8 must take 2
in this case, one of the three blocks in the structure is missing the referenced number, but we know that the possibilities for a solution are pushed to a set of three cells, all in one row or column
if this set has a couple of numbers given or solved then this is the case, our hidden single exists in the 3rd cell
* a second case
is when 2 appearances of a number exist in blocks that do not relate, but even though they may not relate, there is always a block that relates to both, it is the block where the block-row containing the first cell is crossed with the block-column containing the second
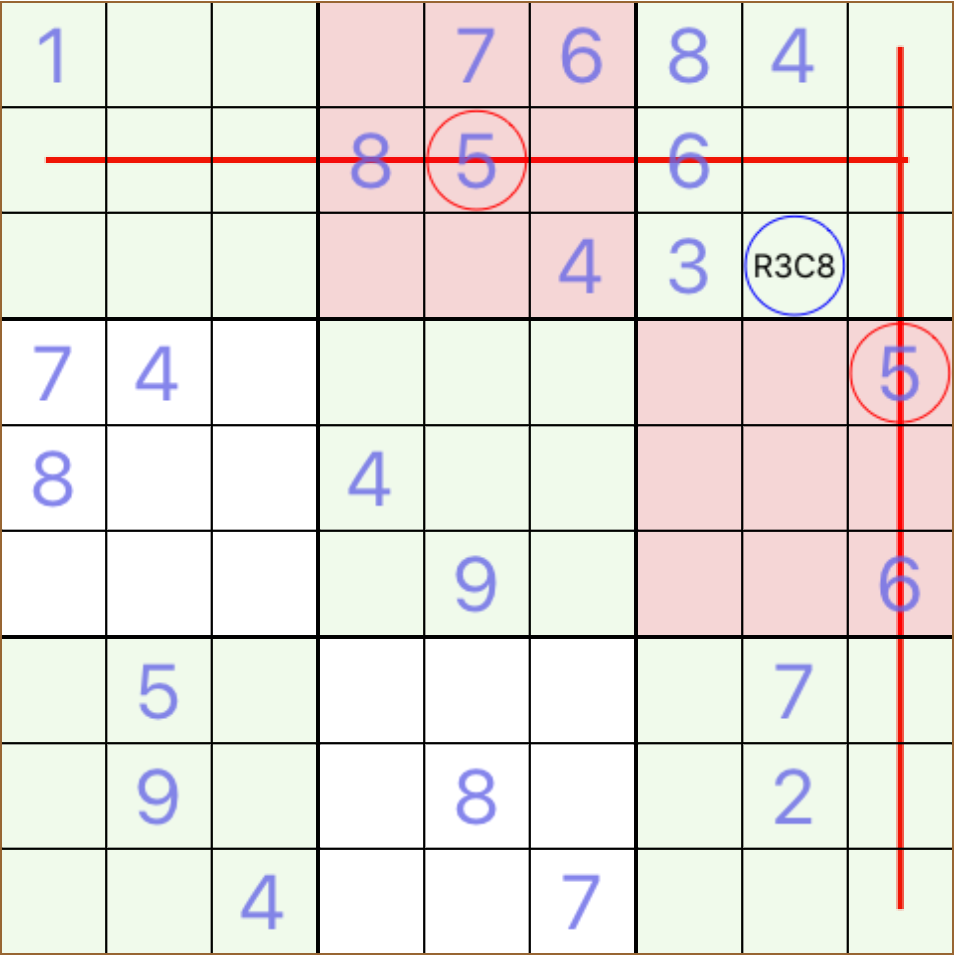
R3C8 must take 5 the conjunction in this block leaves 4 cells not related in any way to the initially referenced cells when 3 of them are given or solved then the 4th must contain our hidden single * a third case is when one block in cooperation with a row or column eliminate all empty cell, but one, in a row or column, from having a particular candidate
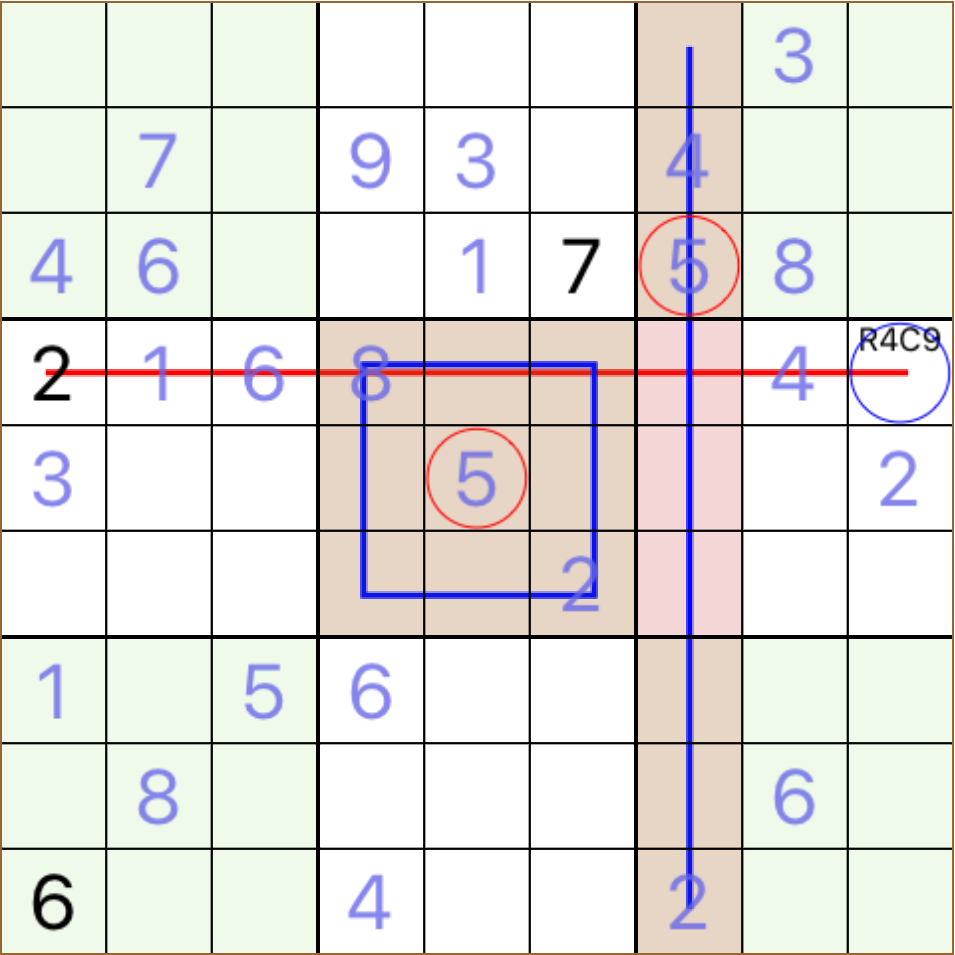
R4C9 must take 5
some more cases
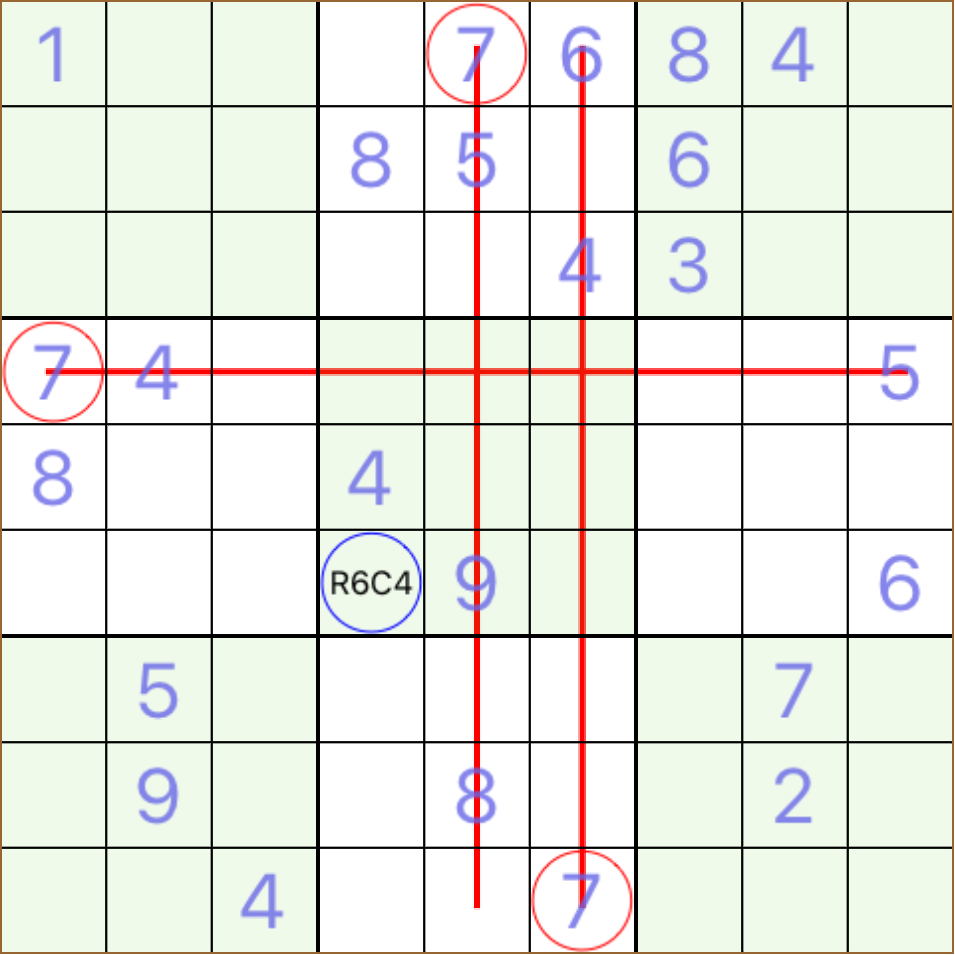
R6C4 must take 7
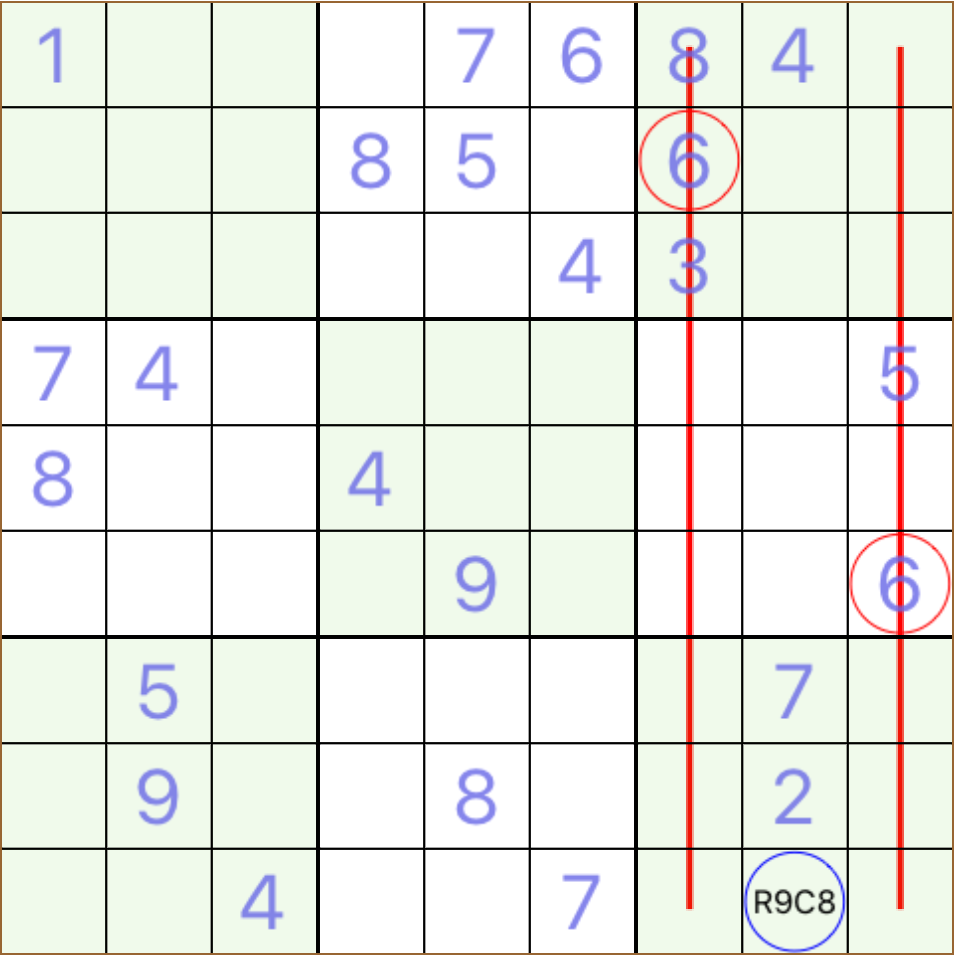
R9C8 must take 6
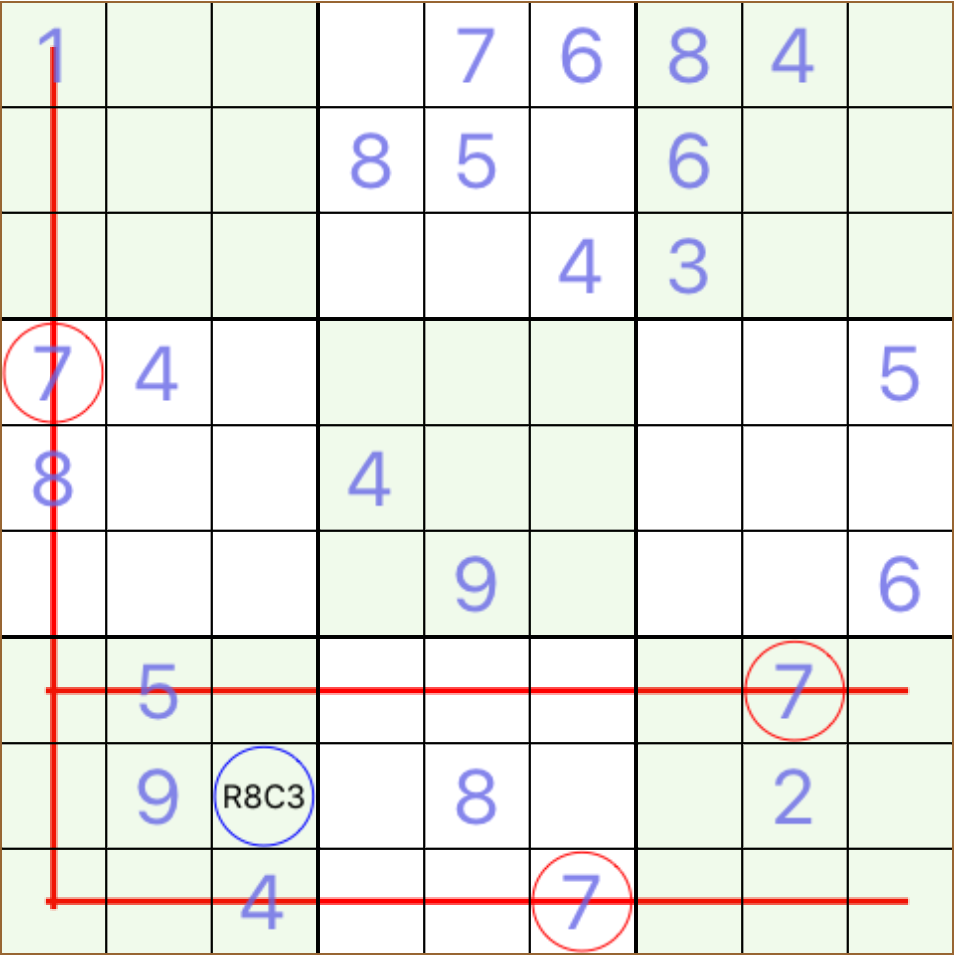
R8C3 must take 7
be a sudoker
some providers list as easy, puzzles containing only naked singles, as medium, puzzles containing mostly naked and some hidden singles and as hard, puzzles containing mostly hidden singles using the skills acquired so far from this tutorial, you are able to solve any sudoku puzzle of size 9x9 listed as easy, medium or hard *** you can confirm this create a blank grid from the puzzles' organiser, then input the numbers one by one of a puzzle listed as hard from any source (magazine, web etc), then try to solve it. you will realise that you have new skills but the aim of this tutorial is to exceed these skills and reach the level of solving beatific puzzles. those known so far as evil, extreme, insane etc this is the case where there are neither naked nor hidden singles in our puzzle solving a puzzle is not guessing the solution but providing logical sequences that reach the solution so in this case where we cannot imply the solution for any cell, we are not allowed to make any guesses what can we do ? here is a secret when there are no singles, we may be able to create some how ? singles are implied by the elimination of a candidate from a set of cells leaving space to only one cell we'll find that this is worthy not only when we catch a naked single, but also when we just reduce the number of candidates for a particular cell by eliminating some of them accumulating eliminations is the path to reach new singles and ultimately solve the puzzle this path is explored in the next section
Advanced techniques
this section describes the techniques necessary for solving every sudoku puzzle with a unique solution, despite its difficulty level, and a way to provide a logically documented solution the puzzles generated by this program require at least one application of these techniques the absolutely required applications are listed in the puzzle's description in the organiser and only these count for valuing the puzzle's difficulty level even though, during solving the puzzle, you may find other applications that you may forward the following techniques are listed according to priority provided by the algorithm
Subsets
***
Block Interaction
***
Block to Block Interaction
***
X-Wing
***
XY-Wing
***
XYZ-Wing
***
XY-Chain
***
Forcing Chain
***
Swordfish
***
Coloring
***
Remote Pairs
***